特徴量が多すぎる？主成分分析を見てみましょう

Too many features? Let's take a look at Principal Component Analysis.

自家製の機械学習モデルシリーズ

こちらのコンパニオン・レポジトリが利用可能です！

次元の呪いは、機械学習における主要な問題の1つです。特徴量の数が増えるにつれて、モデルの複雑さも増します。さらに、十分なトレーニングデータがない場合、オーバーフィッティングが発生します。

この記事では、主成分分析（PCA）を紹介します。まず、なぜ特徴量が多すぎると問題になるのかを説明します。次に、PCAの背後にある数学とその効果を説明します。さらに、視覚的な例とコードスニペットに伴うステップごとにPCAを分解します。さらに、PCAの利点と欠点について説明します。最後に、これらのステップを後で使用するためにPythonクラスにカプセル化します。

読者への注意：数学的な説明に興味がなく、実際の例とPCAの動作を見たい場合は、「PCA in practice」セクションにジャンプしてください。Pythonクラスに関心がある場合は、「Home-brewed PCA implementation」に進んでください。

• チャットGPTの潜在能力を引き出すためのプロンプトエンジニアリングのマスタリング
• 数字の向こう側：データ分析におけるソフトスキルの重要な役割
• 紛争のトレンドとパターンの探索：マニプールのACLEDデータ分析

特徴量が多すぎる問題とは？

図1の特徴空間を見てください。すべての空間を埋めるための例が少ないため、このデータのモデルは、新しい、未知の例に対して一般化できない可能性があります。

別の特徴を追加した場合、どうなるでしょうか？図2の新しい特徴空間を見てみましょう。前の例よりさらに多くの空きスペースがあることがわかります。特徴量の数が増えるにつれて、モデルは現在のデータにオーバーフィットします。そのため、データの次元数を減らすための技術があります。[1]

PCAの目的とは？

簡単に言えば、PCAの目的は、元のデータから情報を最大限に保持する低次元の新しい相関のない特徴を抽出することです。この文脈での情報の尺度は分散です。なぜかを見てみましょう：

この技術は、私たちのd次元のデータポイントxが、直交基底のベクトルの線形結合で表されるという仮定に基づいています[1]：

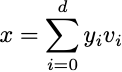
心配しないでください。後で、この基底のベクトルがどこから来たのかを説明します。さらに、組み合わせの中からm個のベクトルを使用してx̂の表現を抽出できます（m < d）：

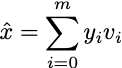
もちろん、特徴量が少ないため正確な表現を得ることはできませんが、少なくとも情報の損失を最小限に抑えようとします。元の例xと近似値x̂の平均二乗誤差（MSE）を定義しましょう：

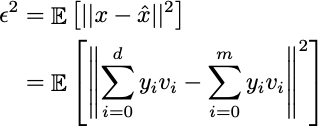
両方の和が異なる変数を使用しているため、差はオフセットにすぎません：

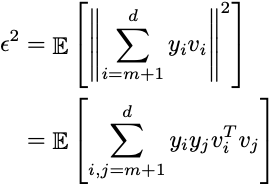
xが直交正規ベクトルの合計であることを仮定しています。したがって、これらのベクトルの内積はゼロであり、各々のユークリッドノルムは1であるため：

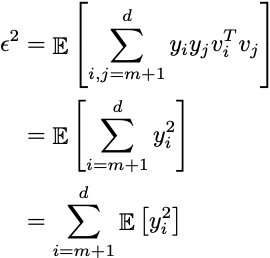
重要度値yiを解決すると：

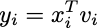
その結果を期待値に代入すると：

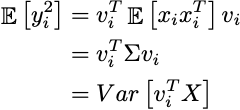
xiが中心化されている（平均がゼロの場合）、期待値はデータ全体の共分散行列であり、この結果は元の空間の分散にすぎません。最適なベクトルviを選択することで分散を最大化し、表現エラーを効果的に最小化できます。

この直交正規ベクトルはどこから来るのか？

先に述べたように、分散を最大化するm個のベクトルを取得したいのです：

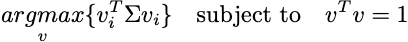
データ行列全体を取ると、viが投影方向であることがわかります。データは、より低次元の空間に投影されます。

共分散行列Σを固有値分解を使用して対角化すると：

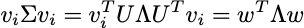
ここで、UはΣの正規化された固有ベクトルを含む行列であり、ΛはΣの固有値を降順で含む対角行列です。これは、Σが実数対称行列であるため可能です。

さらに、Λは対角線上にのみ非ゼロ値を含むため、上記の式を次のように書き直すことができます：

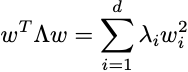
ただし：

Uのベクトルとベクトルvは正規化されています。そのため、各vとaの二乗ドット積を実行すると、値は[0,1]の間にあり、wも正規化されたベクトルである必要があります：

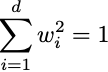
ここから、興味深い特性が現れます。

第一主成分

最適化問題を思い出してください。固有値が順序付けられ、wが正規化されたベクトルである必要があるため、最良のオプションは、w =（1,0,0、…）を持つ最初の固有ベクトルを取得することです。その結果、上限は次の場合に達成されます：

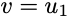
分散を最大化する射影方向は、最大の固有値に関連する固有ベクトルであることが判明しました！

残りの成分

最初の主成分が設定されたら、最適化問題に新しい制限が加えられます：

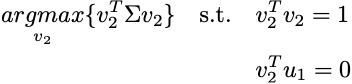
これは、新しい成分v2が前の成分である固有ベクトルu1に直交する必要があることを意味します。したがって、情報が重複しないようになります。証明することができます。すべてのd成分は、降順に関連するΣから正規化されたd個の固有ベクトルに対応します。この主張の形式的な証明については、これらのノートを参照してください[2]。

実践におけるPCA

上記の理論的説明から、データセットの主成分を取得するために必要な手順を説明できます。初期データセットを次の2D正規分布のランダムサンプルとします：

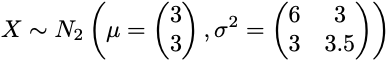
from scipy import statsmean = [3,3]var = [[6, 3],       [3, 3.5]]n = 100data_raw = np.random.multivariate_normal(mean, var, 100)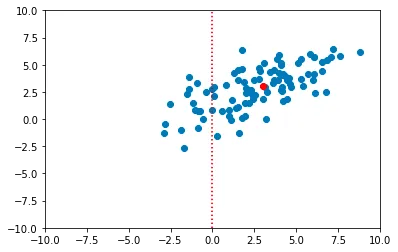

1. データの中心化

最初のステップは、データがゼロ平均を持つように、クラウドを座標系の原点に移動することです。このステップは、データセット内のすべての点からサンプル平均を減算することによって実行されます。

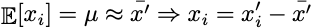
import numpy as npdata_centered = data_raw - np.mean(data_raw, axis=0)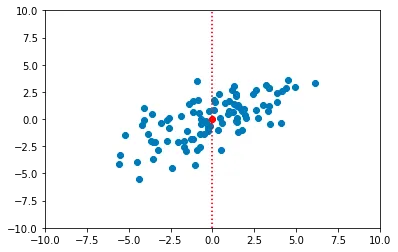

2. 共分散行列の計算

上記で定義された分散は、母集団の共分散行列Σです。実際には、その情報は利用できません。1つのサンプルしか持っていないためです。したがって、サンプル共分散Sを使用して、そのパラメーターを近似できます。

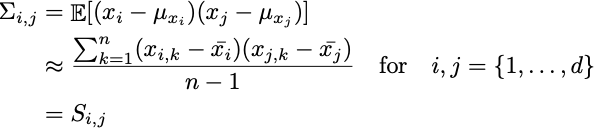
すでにデータが中心化されていることに注意してください。したがって：

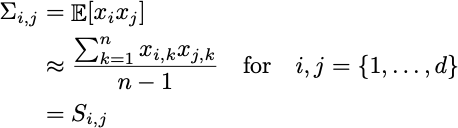
これを行列乗算を使用してコンパクトに書くことができます。これは、計算をベクトル化するのにも役立ちます。

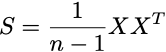
cov_mat = np.matmul(data_centered.T, data_centered)/(len(data_centered) - 1)# > array([[5.62390186, 2.47275007],# >       [2.47275007, 3.19395349]])

コードで転置行列を最初の引数として渡す理由は、データ行列の数式的な定式化において、特徴量が行に、被験者が列にあるためです。実装では、ほとんどのシステムで、イベント、被験者、ログなどが行に格納されるため、逆のことが起こります。

3. 共分散行列の固有分解を実行する

固有値と固有ベクトル a は、scipy の eig() を使用して計算されます：

from scipy.linalg import eigheigvals, eigvecs = eigh(cov_mat)# 固有値と固有ベクトルをソートindices = eigvals.argsort()[::-1]eigvals, eigvecs = eigvals[indices], eigvecs[:,indices]eigvecs# > array([[-0.82348021,  0.56734499],# >        [-0.56734499, -0.82348021]])

前述の通り、固有値は主成分の分散を表し、固有ベクトルは射影方向を表します：

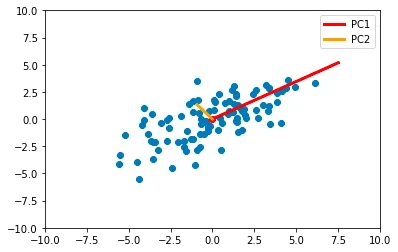
主成分の方向を使用して新しい座標系が作成されることがわかります。さらに、固有値と固有ベクトルは新しいデータを変換するために保存する必要があります。

4. 決定論を強制する

固有ベクトルの係数は、その符号を除いて常に同じです。PCA には複数の有効な向きがある可能性があるため、各列について固有ベクトル行列を取り、その列内の最大絶対値の符号を適用することで、決定論的な結果を強制する必要があります。

max_abs_cols = np.argmax(np.abs(eigvecs), axis=0)signs = np.sign(eigvecs[max_abs_cols, range(eigvecs.shape[1])])eigvecs = eigvecs*signseigvecs# > array([[ 0.82348021, -0.56734499],# >      [ 0.56734499,  0.82348021]])

5. 新しい特徴量を抽出する

各新しい特徴量（主成分）は、元の特徴空間の各点と固有ベクトルのドット積を計算することによって抽出されます：

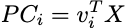
new_features = np.dot(data_centered, eigvecs)

この特定の例では、コンポーネントを計算した後、空間内の新しい点は次のように描かれます：

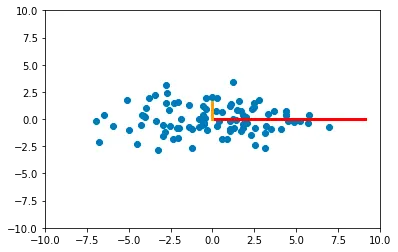
この結果は、基本的には属性が相関していない原点群の回転であることに注意してください。

6. 次元削減

これまで、主成分はビジュアル的に理解するために完全に計算されています。残りのタスクは、必要なコンポーネントの数を選択することです。各主成分の分散を表す固有値を使用することで、このタスクに戻ります。

コンポーネント i が保持する分散の比率は次の式で与えられます：

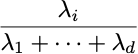
そして、m個のコンポーネントを選択することによって保存される分散の比率は次のようになります：

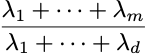
例えば、各成分の分散を視覚化すると、次のようになります：

# 各個々のコンポーネントの分散を棒グラフとして表示plt.bar(    [f"PC_{i}" for i in range(1,len(eigvals)+1)],    eigvals/sum(eigvals))# m個のコンポーネントが保有する割合を赤い線で表すplt.plot(    [f"PC_{i}" for i in range(1,len(eigvals)+1)],    np.cumsum(eigvals)/sum(eigvals),    color='red')plt.scatter(    [f"PC_{i}" for i in range(1,len(eigvals)+1)],    np.cumsum(eigvals)/sum(eigvals),    color='red')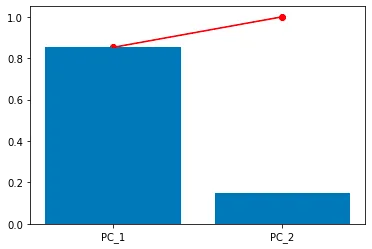

この場合、PC1は元のデータの分散の80％を表し、残りの20％はPC2に属します。さらに、最初の主成分だけを使用することを選択することができます。その場合、データは次のようになります：

これは最初の固有ベクトルの方向にデータを投影したものです。現時点ではあまり役に立っていません。代わりに、3つのクラスに属するデータを選択した場合、PCAはどのようになるでしょうか？

マルチクラスデータ上のPCA

線形分離可能な3つのクラスを持つデータセットを作成しましょう：

from sklearn.datasets import make_blobsX, y = make_blobs()plt.scatter(X[:,0], X[:,1],c=y)plt.legend()plt.show()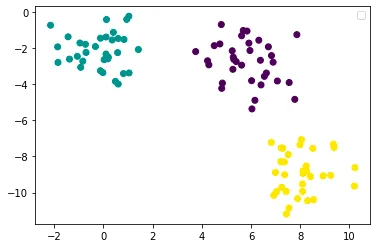

上記のデータにPCAを適用すると、主成分のプロットが次のようになります：

そして、最初のコンポーネントのプロット（最大固有値に対応する固有ベクトルの方向にデータを投影したもの）は次のようになります：

うまくいった！データはまだ線形モデルによって容易に分離できるように見えます。

利点と欠点

科学において、銀の弾丸はありません。実世界のデータでPCAを使用する前に、考慮すべき利点と欠点のリストがあります。

PCAの利点

1. 次元削減: PCAは、重要な情報のほとんどを保持しながら、高次元データを低次元空間に削減することができます。これは、データの可視化、計算効率、次元の呪いに対処するために役立ちます。
2. デコレーション: PCAは、元の変数を主成分と呼ばれる新しい無相関変数のセットに変換します。このデコレーションは解析を簡素化し、機械学習アルゴリズムの独立性を前提とする下流のパフォーマンスを向上させることができます。
3. ノイズ除去: PCAによって得られる低次元表現は、ノイズを除去し、データの最も重要な変動に焦点を当てる傾向があります。これにより、信号対雑音比が向上し、後続の解析の堅牢性が向上する可能性があります。

PCAの欠点

1. 線形性の仮定: PCAは、基礎となるデータ関係が線形であると仮定しています。データが複雑な非線形関係を持つ場合、PCAは最も意味のある変動を捕捉できず、最適な結果を提供できない可能性があります。
2. 解釈可能性: PCAから得られる主成分は、元の特徴量の線形結合です。主成分を元の変数に関連付け、その正確な意味を理解することは困難です。
3. スケーリングへの感度: PCAは、入力変数のスケーリングに敏感です。変数のスケールが異なる場合、分散が大きい変数が解析を支配し、バイアスのある結果をもたらす可能性があります。信頼性の高いPCAの結果を得るには、適切な特徴スケーリングが重要です。
4. 外れ値: PCAは、データの分散に焦点を当てるため、外れ値に敏感です。外れ値は主成分に大きな影響を与え、結果を歪める可能性があります。

自作PCA実装

主成分分析の詳細を説明したので、上記の動作をカプセル化し、将来の問題で再利用できるクラスを作成することが残されています。

この実装では、以下のメソッドが使用されます。

• fit()
• transform()
• fit_transform()

コンストラクタ

複雑なロジックは必要ありません。コンストラクタは、変換されたデータが持つ次元（特徴）の数を定義するだけです。

import numpy as npfrom scipy.linalg import eighclass PCA:    """Principal Component Analysis.    """    def __init__(self, n_components):        """PCAクラスのコンストラクタ。        パラメータ：        ===========        n_components：int            変換されたデータの次元数。            n_features以下である必要があります。        """        self.n_components = n_components        self._fit_instance = False

フィットメソッド

フィットメソッドは、前節のステップ1〜4を適用します。

• データの中心化
• 共分散行列の計算
• 固有値、固有ベクトルの計算とソート
• 固有ベクトルの符号を反転して決定論を強制する

また、固有値とベクトル、およびサンプル平均をオブジェクト属性として保存し、後で新しいデータを変換するために使用します。

    def fit(self, X):        """データを変換するための固有ベクトルを計算する        パラメータ：        ===========        X：[n_examples、n_features]のnp.array            データ行列                戻り値：        ===========        なし        """        # データの平均値をフィットして中心化する        self.mean = np.mean(X, axis=0)        X_centered = X - self.mean        # 共分散行列を計算する        cov_mat = np.matmul(X_centered.T, X_centered)/(len(X_centered) - 1)        # 固有値、固有ベクトルを計算してソートする        eigenvalues, eigenvectors = eigh(cov_mat)        self.eigenvalues, self.eigenvectors = self._sort_eigen(eigenvalues, eigenvectors)        # 説明された分散比を取得する        self.explained_variance_ratio = self.eigenvalues/np.sum(self.eigenvalues)                # 固有ベクトルを反転して決定論を強制する        self.eigenvectors = self._flip_eigenvectors(self.eigenvectors)[:, :self.n_components]        self._fit_instance = True

The transform method

このメソッドは、ステップ1、5、6を適用します：

• 保存されたサンプル平均を使用して新しいデータを中心に配置する
• 新しいPC特徴を抽出する
• n_components次元を選択して次元を削減する。

    def transform(self, X):        """データを固有ベクトルの方向に射影します。        Parameters:        ===========        X: np.array of shape [n_examples, n_features]            データ行列                Returns:        ===========        pcs: np.array[n_examples, n_components]            PCAからの新しい、相関のない特徴量。        """        if not self._fit_instance:            raise Exception("PCAは最初にデータに適合させる必要があります！ fit()を呼び出してください")               X_centered = X - self.mean        return np.dot(X_centered, self.eigenvectors)

The fit_transform method

実装の簡単さのために、このメソッドは最初にfit()関数を適用し、後でtransform()関数を適用します。もっと賢い定義を考え出せるはずです。

def fit_transform(self, X):       """PCAを適合させ、データを変換します。       """       self.fit(X)       return self.transform(X)

ヘルパー関数

これらのメソッドは、コードをより読みやすく、保守しやすくするために、すべてのステップをfit()関数で適用する代わりに、別々のコンポーネントとして定義されました。

    def _flip_eigenvectors(self, eigenvectors):        """固有ベクトルの符号を変更して決定論を強制します。        """        max_abs_cols = np.argmax(np.abs(eigenvectors), axis=0)        signs = np.sign(eigenvectors[max_abs_cols, range(eigenvectors.shape[1])])        return eigenvectors*signs        def _sort_eigen(self, eigenvalues, eigenvectors):        """固有値を降順にソートし、対応する固有ベクトルをソートします。        """        indices = eigenvalues.argsort()[::-1]        return eigenvalues[indices], eigenvectors[:, indices]

クラスのテスト

PCAクラスを使用した前の例を使ってみましょう：

from pca import PCA# 自分自身の著書からPCAのクラスを使用するpca = PCA(n_components=1)X_transformed = pca.fit_transform(X)# 最初のPCをプロットplt.scatter(X_transformed[:,0], [0]*len(X_transformed),c=y)plt.legend()plt.show()

結論

少量のデータで多数の特徴量を持つことは有害であり、おそらく過学習の結果になるでしょう。主成分分析は、この問題を緩和するのに役立つツールです。これは、データの射影方向を見つけることによって機能する次元削減技術であり、元の変動性を可能な限り維持し、結果の特徴量が相関しないようにします。さらに、各新しい特徴量、または主成分が説明する分散を測定できます。その後、ユーザーは、何個の主成分とどの程度の分散がタスクに十分かを選択できます。最後に、PCAは線形に分離可能であり、外れ値に敏感であるサンプルを使用して機能するため、まずデータをよく知っておく必要があります。

参考文献

[1] Fernández, A. Dimensionality Reduction. Universidad Autónoma de Madrid. Madrid, Spain. 2022.

[2] Berrendero, J. R. Regresión lineal con datos de alta dimensión. Universidad Autónoma de Madrid. Madrid, Spain. 2022.

LinkedInで私に連絡してください！

We will continue to update VoAGI; if you have any questions or suggestions, please contact us!