時系列データのフーリエ変換 numpyを使用した高速畳み込みの解説

'Using numpy for fast convolution Explanation of Fourier Transform on Time Series Data'

スクラッチ実装 vs NumPy

フーリエ変換アルゴリズムは、数学の中でも最も偉大な発見の一つとされています。フランスの数学者ジャン＝バティスト・ジョゼフ・フーリエは、1822年の著書「熱の解析理論」で調和解析の基礎を築きました。現代では、フーリエ変換とその派生が、圧縮、通信、画像処理などの技術の基盤となっています。

この素晴らしいフレームワークは、時系列の分析にも優れたツールを提供しています… そして、それが私たちがここにいる理由です！

この投稿は、フーリエ変換に関するシリーズの一部です。今日は畳み込みについて話し、フーリエ変換が畳み込みを行う最速の方法を提供することを紹介します。

すべての図表と式は筆者によって作成されました。

• Falcon AI 新しいオープンソースの大規模言語モデル
• GPT-1からGPT-4まで：OpenAIの進化する言語モデルの包括的な分析と比較
• NVIDIAのCEO、ヨーロッパの生成AIエグゼクティブが成功の鍵を議論

離散フーリエ変換（DFT）の定義

まずは基本的な定義から始めましょう。離散時間信号 x の離散フーリエ変換は次のように表されます：

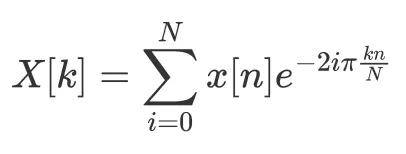
ここで、k は x のスペクトルの k 番目の周波数を示します。注意点として、一部の著者はこの定義に1/Nのスケーリング係数を追加していますが、この記事においてはそれほど重要ではありません。全体として、それは定義の問題であり、それに固執するだけのことです。

逆フーリエ変換は、順方向フーリエ変換の定義に基づいて次のように表されます：

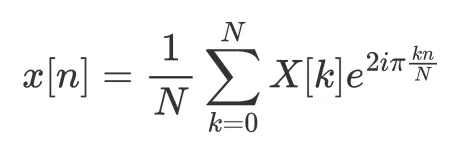
それは言えることですが、フーリエ変換に関する最も重要な定理の一つは、一方の空間での畳み込みがもう一方の空間での乗算と等価であることです。言い換えれば、積のフーリエ変換は、それぞれのフーリエスペクトルの畳み込みであり、畳み込みのフーリエ変換はそれぞれのフーリエスペクトルの積です。

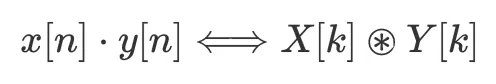
および

ここで、ドットは通常の積（乗算）を表し、丸で囲まれた星は循環畳み込みを表します。

2つの重要なポイント：

• 周期信号：フーリエ解析フレームワークでは、扱う信号が周期的であると考えられています。言い換えれば、それらはマイナス無限大から無限大まで繰り返されます。ただし、有限のメモリを持つコンピュータでそのような信号を扱うことは常に実用的ではないため、ここでは1周期だけを扱います。
• 循環畳み込み：畳み込みの定理によれば、乗算は循環畳み込みに相当し、これは私たちがより馴染みのある線形畳み込みとは少し異なるものです。しかし、それほど異なるわけではなく、複雑ではありません。

循環畳み込み vs 線形畳み込み

もし線形畳み込みに慣れているなら、循環畳み込みに混乱することはありません。基本的に、循環畳み込みは周期信号の畳み込み方法です。線形畳み込みは有限長の信号にのみ意味があり、マイナス無限大からプラス無限大まで広がる信号には適用できません。フーリエ解析の文脈では、信号は周期的であるため、この条件を満たしません。従って、（線形）畳み込みについては話すことができません。

しかし、周期信号に対しては、線形畳み込みに似た操作を直感的に考えることができます：周期信号を1周期の長さで畳み込むだけです。これが循環畳み込みが行うことです：同じ長さの2つの周期信号を1周期の範囲で畳み込みます。

さらに違いを確認するために、離散線形畳み込みと離散循環畳み込みの式を比較してみましょう：

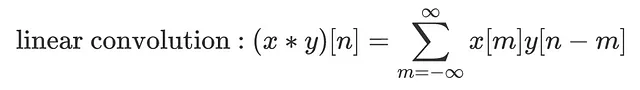
次の違いに注意してください：

– 範囲：線形畳み込みはマイナス無限大からプラス無限大までのサンプルを使用します。前述のように、この文脈ではxとyは有限のエネルギーを持つため、和が意味を持ちます。循環畳み込みでは、1周期の範囲で何が起こったかだけを知る必要があるため、和は1周期に限定されます。

– 循環インデックス：循環畳み込みでは、yのインデックスをNの長さでモジュロ演算を用いて「ラップ」します。これは、yが周期Nで周期的であることを保証するための方法です：位置kでのyの値を知りたい場合、位置k%Nのyの値を使用するだけです。yがN周期的であるため、正しい値が得られます。これも、周期的な無限長のサンプルシーケンスを扱うための数学的な方法です。

NumPyでの実装

NumPyは有限長信号に対する優れたツールを提供しています。これは良いニュースです。なぜならば、先ほど見たように、無限長の周期信号は単一の周期で表現できるからです。

このような信号を表すためのシンプルなクラスを作成しましょう。配列を簡単にプロットするためのメソッドを追加し、基本的な配列の前後に追加の周期を付け加えて、周期的なシーケンスであることを示します。

2つの例を見てみましょう：まずはサンプリングされた正弦波のシーケンス、次に線形シーケンスです。どちらもN周期的（この場合はN=10）と見なされます。

循環畳み込み、遅い方法

では、先ほど見た循環畳み込みの式を実装してみましょう。インデックスとモジュロ演算子を使用すると、非常に簡単です：

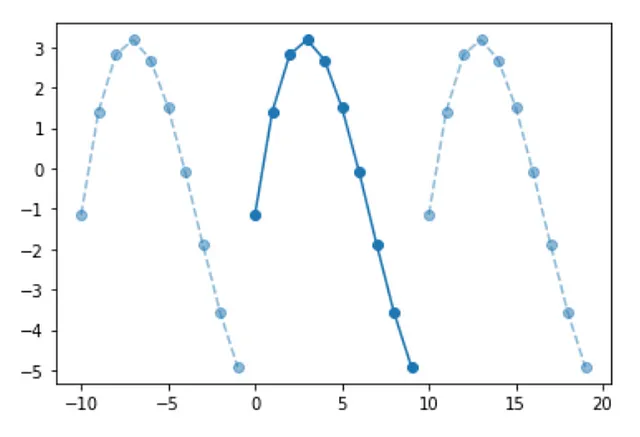
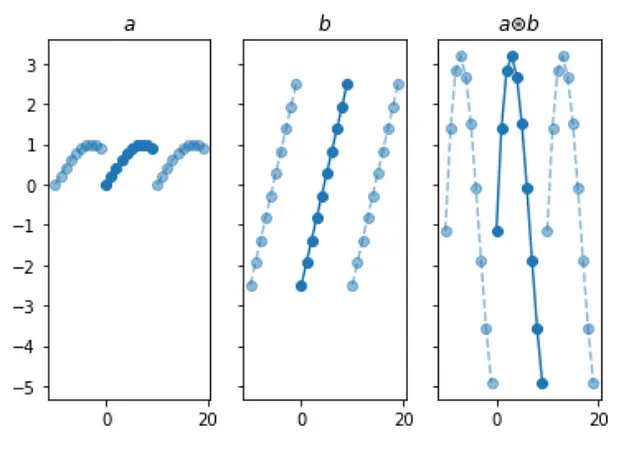
それは素晴らしいですね、2つのシグナル間の循環畳み込みの様子が見えるようになりました。すべてを1つの図にまとめます：

この解決策は非常にうまく機能しますが、大きな欠点があります：遅いということです。ご覧のように、結果を計算するために2つのネストされたループを実行する必要があります。結果配列の各位置に対して、その位置での結果を計算するためのループです。このアルゴリズムはO(N²)と呼ばれます。Nが増えるにつれて、操作の数はNの2乗に比例して増加します。

例のような小さな配列では問題ありませんが、配列が大きくなると深刻な問題になります。

さらに、数値データのループはPythonではほとんどの場合、悪いプラクティスとされています。もっと良い方法があるはずです…

循環畳み込み、フーリエの方法

そして、それがフーリエ変換と畳み込み定理が登場する場所です。離散フーリエ変換が非常に高速かつ最適化された方法で実装されるため、操作は非常に速いです（FFTはO(N log N)と言われており、O(N²)よりもはるかに良いです）。

畳み込み定理を使用すると、2つのシーケンスのDFT（離散フーリエ変換）の積を逆DFT（逆フーリエ変換）を使用して時間領域に戻すと、入力時間シーケンスの畳み込みが得られます。言い換えれば、次のようになります：

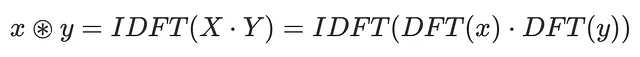
ここで、DFTは離散フーリエ変換を表し、IDFTは逆操作を表します。

次に、numpyを使用してxとyの畳み込みを計算するためにこのアルゴリズムを簡単に実装できます：

数値と時間の比較

最後に、両方のアプローチが同じ結果をもたらし、Pythonが両方のテクニックを使用して循環畳み込みを計算するのにかかる時間を比較してみましょう：

<img alt="2つの周期的なシーケンス間の循環畳み込みを計算するための両方のアプローチの比較：青色の「遅い方法」はループと加算を使用した単純な代数的な方法で、オレンジ色の「フーリエの方法」と重ね合わせられています。両方の方法は、数値の精度まで正確に等しい結果を提供します（著者による作成）。

完全に一致しています！数値値の観点で厳密に等価です。

さて、時間の比較です：

結果は次のとおりです：

• N=10のサンプルの場合、DFTは約6倍速いです
• N=1000のサンプルの場合、DFTは約10000倍速いです

それはすごいです！数千ものサンプルを持つ時系列データを分析する際にどのような効果があるか考えてみてください！

まとめ

この投稿では、フーリエ変換が強力なツールであること、特に畳み込み定理によって非常に効率的な方法で畳み込みを計算できることを見てきました。線形と循環は正確には同じ操作ではありませんが、両方とも畳み込みに基づいています。

フーリエ変換に関する将来の投稿を直接フィードで受け取るために購読してください！

また、他の投稿もチェックしてください。好きなものがあれば、購読していただけると私が100人の購読者の目標に到達するのにとても助かります：

NumPyを使用した有限差分法の解像度を300倍高速化 | Yoann Mocquin著 | Towards Data Science (VoAGI.com)

PCA/LDA/ICA：コンポーネント分析アルゴリズムの比較 | Yoann Mocquin著 | Towards Data Science (VoAGI.com)

NumPyの配列をラッピングする。コンテナのアプローチ。| Yoann Mocquin著 | Towards Data Science (VoAGI.com)

Seabornの詳細：カラーパレット | Yoann Mocquin著 | Analytics Vidhya | VoAGI

We will continue to update VoAGI; if you have any questions or suggestions, please contact us!