ディープラーニングのためのPythonとC++による自動微分
PythonとC++での自動微分によるディープラーニング
この記事では、トレーニングループ中にパラメータの勾配を自動的に計算する現代のDeep Learningフレームワークの機能である自動微分について探求します。この記事では、PythonとC++を使用した具体的な例を交えて、この技術を紹介します。

ロードマップ
- 自動微分:何か、動機など
- PythonでのTensorFlowを使用した自動微分
- C++でのEigenを使用した自動微分
- 結論
自動微分
PyTorchやTensorFlowなどの現代のフレームワークには、自動微分[1]と呼ばれる機能があります。その名前からもわかるように、自動微分は関数の導関数を自動的に計算し、開発者の責任を軽減します。
自動微分の関連性は何ですか?
現代のディープラーニングフレームワークでは、自動微分を使用して訓練可能なパラメータの勾配を計算します。
自動微分が広く利用可能になる前は、モデルの開発には大部分の時間が勾配の計算コードの実装(または実際にはデバッグやバグの除去)に費やされていました。
- 「このGSAi中国のAI論文は、LLMベースの自律エージェントの包括的な研究を提案しています」
- 「人間と機械の対話を革新する:プロンプトエンジニアリングの出現」
- 「メールの生産性を革新する:SaneBoxのAIがあなたの受信トレイの体験を変える方法」
そのため、自動微分はディープラーニングの普及においてゲームチェンジャーとなりました。これにより、堅固な微積分の知識を持たない開発者でも複雑な機械学習アルゴリズムを自信を持って実装することができるようになりました。微積分の知識がある開発者にとっても、自動微分はバグや最適でない実装の可能性を減らしてくれるため、役立ちます。
なぜ自動微分の理解が重要なのですか?
機械学習では、自動微分は勾配の計算を完全に抽象化し、通常はモデル開発者の努力なしに非常に正確で高速な計算を提供します。通常は。ただし、常にそうとは限りません。
数値の不安定性などの要因により、自動微分はごく稀な状況で失敗することがあります。そのため、自動微分の動作原理を理解していると、(i)最も自動微分を活用することができ、(ii)自動微分が失敗したときに検出し、(iii)必要な修正を行うことができます。
また、バックプロパゲーションでは、勾配の計算がより重要でコストのかかる部分であり、自動微分によって完全に実現されています。そのため、自動微分の理解は純粋に必須となります。
TensorFlowを使用した自動微分
GoogleのTensorFlowを使用している場合、レイヤーの導関数を自分で導出することを考えたことはないかもしれません。次に、簡単な例 [2] を紹介します:
import tensorflow as tfclass CustomLayer(tf.keras.layers.Layer): def __init__(self, num_outputs, activation): super(CustomLayer, self).__init__() self.num_outputs = num_outputs self.activation = activation def build(self, input_shape): self.kernel = self.add_weight("kernel", shape=[int(input_shape[-1]), self.num_outputs]) def call(self, inputs): Z = tf.matmul(inputs, self.kernel) Y = self.activation(Z) return Yこのカスタムレイヤーは、バイアスのないtf.keras.layers.Denseのクローンです。次のように使用できます:
def sin_activation(x): return tf.sin(x)my_custom_layer = CustomLayer(2, sin_activation)input = tf.constant([[-1., 0., 1.], [2., 3., 4.], [-1., -5., 2.]])with tf.GradientTape() as tape: output = my_custom_layer(input) loss = tf.reduce_sum(output**2)gradient = tape.gradient(loss, my_custom_layer.trainable_variables)print("my_custom_layer.trainable_variables:\n", my_custom_layer.trainable_variables[0].numpy())print("\ngradient:\n", gradient[0].numpy())このコードは次のような出力を生成します:

組み込みの活性化関数(例:tf.keras.activation.relu)を使用していないため、TensorFlowはその勾配をどのように計算するのでしょうか?答えはシンプルです:自動微分を使用しています。
自動微分の仕組み
sin_activationの明示的な導関数を開発者に提供する代わりに、TensorFlowは自動微分を使用して勾配を計算します。しかし、自動微分はどのように機能するのでしょうか?
微積分の授業で関数の導関数を計算する方法を学んだことがあるかもしれません。自動微分は、その導関数を見つけるために同じルールを使用しているのでしょうか?はい、しかし、あなたが行ったのとは異なる方法で行います。
自動微分の中心的なアイデア[3]は、計算グラフを基本的な操作に分解することです。その基本的な操作では、導関数が単純で既知であるため、チェーンルールを再帰的に適用して最上位の導関数を計算します。
例えば、最後の例で損失がどのように計算されたかを見てみましょう:

この図は、損失値の計算フローを表しています。チェーンルールを使用して、重みに対する損失の勾配の式を求めることができます:

これは次のように簡略化できます:

右側の偏微分は勾配計算グラフの葉です。これらは何らかの意味で基本的であり、他の導関数を導くことはできません。
さて、自動微分はこれらの葉の勾配の値を見つける必要がありますが、これは基本的な微積分のルールを使用して非常に簡単に解決できます:
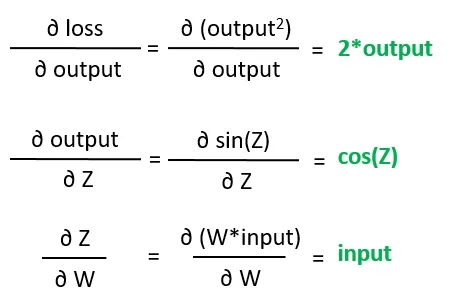
最終的に、損失に対する重みの勾配は次の計算で見つけられます:

自動微分は、開発者の明示的な干渉なしにこのグラフ計算を行います。素晴らしい!では、問題は何でしょうか?問題は詳細にあります!
数値不安定性が影響を及ぼす
この物語の前半で述べたように、いくつかの状況では、中間または葉の勾配の数値不安定性のために自動微分が失敗します。次の例を考えてみてください:
import tensorflow as tfinput = tf.Variable(100.0)def function_using_autodiff(x): return 1./tf.exp(x)with tf.GradientTape() as tape: output = function_using_autodiff(input)gradient = tape.gradient(output, input)print("output using autodiff: ", output.numpy())print("gradient using autodiff: ", gradient.numpy())このプログラムは次のように出力されます:

この場合、関数はx=100で正しく評価されましたが、autodiffによって提供された勾配はnanでした。この問題をカスタム勾配を使用して解決しましょう。まず、関数の式を確認しましょう:
この関数の導関数は次のようになります:
これをカスタム勾配として実装すると、次のようになります [4]:
import tensorflow as [email protected]_gradientdef function_using_customdiff(x): e = tf.exp(x) def grad(upstream): return upstream * -tf.exp(-x) return 1./tf.exp(x), gradwith tf.GradientTape() as tape: output = function_using_customdiff(input)gradient = tape.gradient(output, input)print("output using custom diff: ", output.numpy())print("gradient using custom diff: ", gradient.numpy())今回は、勾配が正しく評価されました:

数値的な不安定性は、対象とする関数の理論的な特性に起因することもあります。たとえば、次の関数の導関数:
は次のようになります:
これは明らかにx = 0のときに未定義ですが、f(0) = 0です!このような場合には、カスタム勾配を使用して便利な(工学的な)解決策を提供することもできます。
Python/TensorFlowでautodiffを使用する方法を理解したので、次はEigenを使用したC++プログラムでこの技術を使用する方法を学びましょう。
Eigenを使用したC++でのAutodiff
Eigenは、C++向けの最も成功した高性能代数ライブラリの1つです。Eigenについて詳しく知りたい場合は、以前のVoAGIのストーリーの1つを読むことをおすすめします。
Eigen Autodiff [5]を使用するのは非常に簡単です。次は、単純ながらも説明的な例から始めましょう。次の関数を考えてみてください:
template<typename T>T my_function(const T& x){ T result = T(1)/(T(1) + exp(-x)); return result;}ここで注意するのは、この関数をテンプレート関数として定義していることです。詳細には触れませんが、テンプレート関数は関数の型の型です。実際には関数ではありません。このようなテンプレートは、異なるデータ型でmy_functionを再利用できるため便利です。
通常、私たちはfloat、double、またはintなどの型を使用して関数を呼び出します。しかし、Eigen Autodiffを動作させるためには、値をEigen::AutoDiffScalarとして渡す必要があります。以下は例です:
#include <iostream>#include <unsupported/Eigen/AutoDiff>int main(int, char **){ Eigen::AutoDiffScalar<Eigen::VectorXd> X; X.derivatives() = Eigen::VectorXd::Unit(1, 0); X.value() = 2.f; auto Y = my_function(X); std::cout << "Y: " << Y << "\n\n"; std::cout << "derivatives:\n" << Y.derivatives() << "\n"; return 0;}ここでのポイントは、ヘッダーunsupported/Eigen/AutoDiffです。このファイルでは、変数Xの型として使用されるEigen::AutoDiffScalar型がEigenによって定義されています。次に以下の2行を再確認してください:
X.derivatives() = Eigen::VectorXd::Unit(1, 0); X.value() = 2.f;これらの行は、Xとそのインデックスの値を設定します。この例ではXが唯一の変数であるため、そのインデックスは0です。
さて、通常通りXをmy_functionに渡すことができます:
auto Y = my_function(X);YもEigen::AutoDiffScalarです。コードで見るように、Yの各偏微分の値はderivatives()配列に格納されています。このコードを実行すると、次の出力が得られます:

Yは関数の出力値とXに関する導関数の両方を保存しています。これらの値が正しいかどうかをどのように知ることができますか?my_functionが実際にはシグモイドの式であることに気づいたかもしれません:

シグモイドの導関数の式は次のようになります:

したがって、シンプルな計算機を使用してσ(2) = 0.8808およびσ’(2) = 0.10499の値を再確認できます。
これは故意に非常にシンプルな例でした。次はもう少し難しいものを試してみましょう。
C++とEigenを使用してCustomLayerを実装する
C++とEigenを使用して、最終的にCustomLayerの例を再度書き直すことができます:
#include <unsupported/Eigen/CXX11/Tensor>template <typename T>Eigen::Tensor<T, 2> CustomLayer(Eigen::Tensor<T, 2> &X, Eigen::Tensor<T, 2> &W, std::function<Eigen::Tensor<T, 2>(Eigen::Tensor<T, 2>&)> activation){ Eigen::array<Eigen::IndexPair<Eigen::Index>, 1> dims = { Eigen::IndexPair<Eigen::Index>(1, 0) }; Eigen::Tensor<T, 2> Z = X.contract(W, dims); Eigen::Tensor<T, 2> result = activation(Z); return result;};ここでは、3つのポイントを強調します:
- 行列ではなくテンソルを使用している。Eigenのテンソルに慣れていない場合は、この記事を読んでください。
- 収縮を行っている。収縮は行列積の多次元一般化です。
- テンプレート関数を使用している。テンプレートクラスも機能します。ポイントは、前の例と同様にテンプレートとして定義することです。
さらに、activationをstd::functionとして渡しています。では、それを定義しましょう:
template <typename T>T sine(T t) { return sin(t);}template <typename T>Eigen::Tensor<T, 2> sin_activation(Eigen::Tensor<T, 2> & P) { Eigen::Tensor<T, 2> result = P.unaryExpr(std::ref(sine<T>)); return result;};ここでもテンプレートを使用しています。ここではすべてが直感的です。単にunaryExprを使用してPをsin(t)関数を使用してマッピングしています。最後に、CustomLayerを呼び出すことができます:
#include <unsupported/Eigen/AutoDiff>
typedef typename Eigen::AutoDiffScalar<Eigen::VectorXf> AutoDiff_T;
int main(int, char **) {
Eigen::Tensor<float, 2> x_in(3, 3);
x_in.setValues({{-1., 0., 1.}, {2., 3., 4.}, {-1., -5., 2.}});
Eigen::Tensor<float, 2> w_in(3, 2);
w_in.setRandom();
Eigen::Tensor<AutoDiff_T, 2> X = convert(x_in);
Eigen::Tensor<AutoDiff_T, 2> W = convert(w_in, 0, w_in.size());
auto Y = CustomLayer(X, W, sin_activation<AutoDiff_T>);
auto output = Y * Y;
auto LOSS = ((Eigen::Tensor<AutoDiff_T, 0>)output.sum())(0);
auto dY_dW = gradients(LOSS, W);
std::cout << "trainable_variables:\n" << W << "\n\n";
std::cout << "gradient:\n" << dY_dW << "\n\n";
std::cout << "output:\n" << output << "\n\n";
std::cout << "loss:\n" << LOSS << "\n\n";
return 0;
}名前の通り、convert関数は元の正準テンソルx_inとw_inをEigen::Tensor<AutoDiff_T, 2>テンソルに変換します。前の例で説明したように、Eigen自動微分のためにEigen::AutoDiffScalar型は必須です。convertは次のように定義されます:
auto convert = [](const Eigen::Tensor<float, 2> &tensor, int offset = 0, int size = 0) {
const int rows = tensor.dimension(0);
const int cols = tensor.dimension(1);
Eigen::Tensor<AutoDiff_T, 2> result(rows, cols);
for (int i = 0; i < rows; ++i) {
for (int j = 0; j < cols; ++j) {
int index = i * cols + j;
result(i, j).value() = tensor(i, j);
if (size) {
result(i, j).derivatives() = Eigen::VectorXf::Unit(size, offset + index);
}
}
}
return result;
};convertを呼び出す際の2行に注目してください:
Eigen::Tensor<AutoDiff_T, 2> X = convert(x_in);
Eigen::Tensor<AutoDiff_T, 2> W = convert(w_in, 0, w_in.size());実際には、Wに関する偏微分のみを求めています。次のセクションでは、Xに関する偏微分の計算方法について説明します。
最終的に、Yにはレイヤーの出力値とWに関する偏微分が含まれます。その後、gradients関数を使用して勾配を展開できます:
auto gradients(const AutoDiff_T &LOSS, const Eigen::Tensor<AutoDiff_T, 2> &W) {
auto derivatives = LOSS.derivatives();
int index = 0;
Eigen::Tensor<float, 2> result(W.dimension(0), W.dimension(1));
for (int i = 0; i < W.dimension(0); ++i) {
for (int j = 0; j < W.dimension(1); ++j) {
float val = derivatives[index];
result(i, j) = val;
index++;
}
}
return result;
}ビルドして実行すると、このコードは次のような出力を生成します:

Python/TensorFlowの例と同様の出力が予想されます。
Xに関する導関数の取得
前の例では、Wの勾配のみを計算しました。もしXの偏微分も計算したい場合、以下の変更を実装する必要があります:
int size = x_in.size() + w_in.size();Eigen::Tensor<AutoDiff_T, 2> X = convert(x_in, 0, size);Eigen::Tensor<AutoDiff_T, 2> W = convert(w_in, x_in.size(), size);このコードは基本的にEigenにXの導関数の追跡を通知します。注意点として、XとWの両方を展開するために、gradients関数も変更する必要があります:
auto gradients(const AutoDiff_T &Y, const Eigen::Tensor<AutoDiff_T, 2> &X, const Eigen::Tensor<AutoDiff_T, 2> &K){ auto derivatives = Y.derivatives(); int index = 0; Eigen::Tensor<float, 2> dY_dX(X.dimension(0), X.dimension(1)); for (int i = 0; i < X.dimension(0); ++i) { for (int j = 0; j < X.dimension(1); ++j) { float val = derivatives[index]; dY_dX(i, j) = val; index++; } } Eigen::Tensor<float, 2> dY_dK(K.dimension(0), K.dimension(1)); for (int i = 0; i < K.dimension(0); ++i) { for (int j = 0; j < K.dimension(1); ++j) { float val = derivatives[index]; dY_dK(i, j) = val; index++; } } return std::make_pair(dY_dX, dY_dK);}これで、gradientsを適切に呼び出す必要があります:
auto [dY_dX, dY_dW] = gradients(LOSS, X, W);XまたはWのいずれかを渡します。これらの変更を行った後、プログラムを再実行すると、以下の出力が得られます:

オートディフの代替手段
このストーリーの最初に「手動で」fourier_activationの勾配を計算した方法は、記号微分として知られています。
記号微分では、プログラム関数を抽象的な数式に変換する必要があります。数式は微積分のルールを用いて微分され、導関数の形式を得ます。最後に、導関数の形式を使用して出力を得ます。このプロセスを実装するプログラムは、一般的なソフトウェアアプリケーションにはあまり効率的ではありません。
オートディフの代替手段として、数値微分があります。数値微分では、微分は対話的な(離散的な)プロセスによって計算されます。数値微分では、微分は有限なステップで近似されます。数値微分の問題点は、このプロセスが必然的な離散化による丸め誤差を導入することです。さらに、数値微分はしばしばオートディフよりも遅いです。
結論
このストーリーでは、ディープラーニングの分野で最先端のトピックの一つであるオートディフについて紹介しました。この技術をオープンソースパッケージに実装した成功は、人工知能の開発と普及において過去20年間での重要な成果です。
特に、Eigen Autodiffがどれだけシンプルで簡潔であるかには驚かされます。残念ながら、それについてはあまり多くのドキュメントがありません。もしこれらの例があなたのユースケースに適していない場合は、EigenのGitLabリポジトリでさらなる例をチェックすることをおすすめします。
参考文献
[1] Baydin et al., Automatic Differentiation in Machine Learning: a Survey, Journal of Machine Learning Research 18 (2018) 1–43
[2] TensorFlow ドキュメント, カスタムレイヤー
[3] Roger Grosse, CSC321 講義 10: Automatic Differentiation, トロント大学 コンピューターサイエンス
[4] TensorFlow ドキュメント, 高度な自動微分
[5] Patrick Peltzer, Johannes Lotz, Uwe Naumann, Eigen-AD: Algorithmic Differentiation of the Eigen Library, ICCS 2020: 第20回国際会議
We will continue to update VoAGI; if you have any questions or suggestions, please contact us!
Was this article helpful?
93 out of 132 found this helpful
Related articles






