SVMの最適化:プライマルとデュアル形式
SVMの最適化
このリンクをクリックした人なら、既にSVMについて知っているはずですが、背後にはたくさんのことがあります。
データサイエンティストにとって、SVMの最適化の双対形式と原始形式を理解することは重要です。これにより、SVMの動作原理を基本的に理解し、SVMモデルから得られる結果を解釈および説明することができます。さらに、この知識はアルゴリズムの選択とカスタマイズに役立ち、データサイエンティストがデータセットのサイズや計算上の制約などの要素に基づいて最適な最適化手法を選択できるようにします。さらに、双対形式と原始形式の理解は、ハイパーパラメータの調整、高度なモデルの解釈、およびSVMアルゴリズムの計算効率の最適化にも役立ちます。
さあ、シートベルトを締めてください。数学の方程式がたくさんあります。
注意: すべての画像は著者に帰属します。
- LangChainとLLMsのための非同期処理
- Sklearnの交差検証の可視化:K-Fold、シャッフル&スプリット、および時系列スプリット
- 「PolarsによるEDA:集計と分析関数のステップバイステップガイド(パート2)」
SVMは二つの方法で定義されています。一つは双対形式で、もう一つは原始形式です。どちらも同じ最適化結果を得ますが、どのようにしてその結果を得るかは非常に異なります。数学に深入りする前に、どちらがいつ使用されるかを説明しましょう。原始形式は、データにカーネルトリックを適用する必要がなく、データセットは大きいが各データポイントの次元は小さい場合に選択されます。双対形式は、データが非常に高い次元を持っており、カーネルトリックを適用する必要がある場合に選択されます。
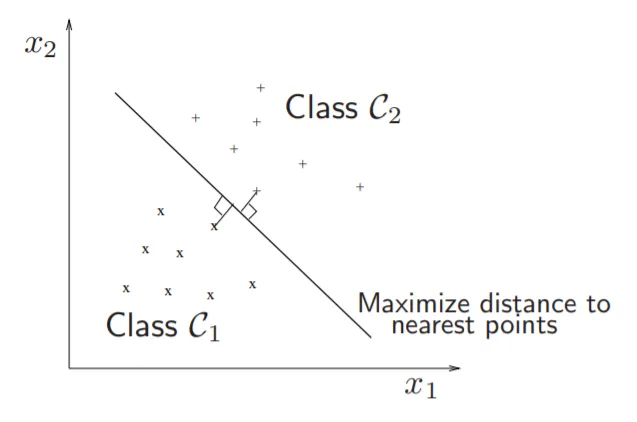
SVMで実際に行っていることを理解しましょう。SVMの最適化では、ハイパープレーンとサポートベクターの距離を最大化することは、重み行列WのL2ノルムを最小化することと同じです。数学を見ていくと、サポートベクターとは実際に何なのかを定義します。しかし、なぜ距離を最大化することが重み行列を最小化することに等しいのでしょうか?
• クラス間のマージンは2 / ||w||_2です。
• ||w||_2を最小化することは、マージンを最大化することに対応します。
• 注意: w’ x1 + b = 1 および w’x2 + b = − 1
⇒ w’(x1* − x2*) = 2 ⇒ w’( x1* − x2*)/||w||_2 = 2 /||w||_2
ここで、x1*とx2*は異なるクラスのハイパープレーン内の最も近い点であり、||w||_2は重み行列のL2ノルムです。
We will continue to update VoAGI; if you have any questions or suggestions, please contact us!
Was this article helpful?
93 out of 132 found this helpful
Related articles






