PageRankによる大規模グラフの分析

大規模グラフの分析' (Analysis of large-scale graphs)

Google検索エンジンがリンク構造に基づいてドキュメントの順位を付ける方法を発見する

順位付けは機械学習の重要な課題です。与えられたドキュメントの集合を特定の基準に基づいて特定の順序で並べることが目標です。順位付けは、情報検索システムで検索結果をソートするために広く使用されるか、特定のユーザーにとって興味深いコンテンツをフィルタリングするための推奨システムで使用されます。

与えられた問題と目標に基づいて、多くの順位付けアルゴリズムが存在します。この記事で学ぶアルゴリズムは「PageRank」と呼ばれるものです。その主な目的は、ドキュメント（ウェブページ）の集合を、それらの接続情報を使用して順位付けすることです。各ウェブページに割り当てられる順位は、その重要性を示します。順位が高いほど、重要性も高くなります。このアルゴリズムは、次のセクションで見ていく2つの仮定に基づいています。

仮定

ウェブページの「重要性」を定義するために、2つの仮定を立てることができます。

• IDEにAIを統合する
• Langchain 101 構造化データ（JSON）の抽出
• VoAGIニュース、8月9日：ChatGPTを忘れて、この新しいAIアシスタントは遥かに進んでいます•データクリーニングと前処理技術の習得のための7つのステップ

他の多くのウェブページがそれを指している場合、ウェブページの重要性は高くなります。

例えば、人気のある研究論文があり、他の記事が引用したり、その結果を使用したりすることでそれにリンクしている場合、この記事には大きな重要性を与えることが合理的です。一方、他のリソースからリンクされていない不明なウェブページがある場合、そのページには重要性が低いと考えられます。

実際には、入力リンクの品質にも注意を払う必要があります。

ウェブページの重要性は、それを指しているウェブページの重要性に比例します。

もしページがウィキペディアの優れた記事によって引用されている場合、そのリンクには大きな重みを持つべきです。逆に、絶対に知られていないリソースが他のウェブページを指している場合、通常は高い重要性を持つべきではありません。

形式的な定義

あるノードの重要性は、入力リンクの重みの合計と等しいとします。

重要性 rᵢ を持つノード i が k 個の出力リンクを持つ場合、各リンクの重みをどのように決定すればよいでしょうか？もっとも直接的なアプローチは、ノードの重要性を出力リンクの数で均等に分割することです。これにより、各出力リンクは rᵢ / k の重みを受け取ります。

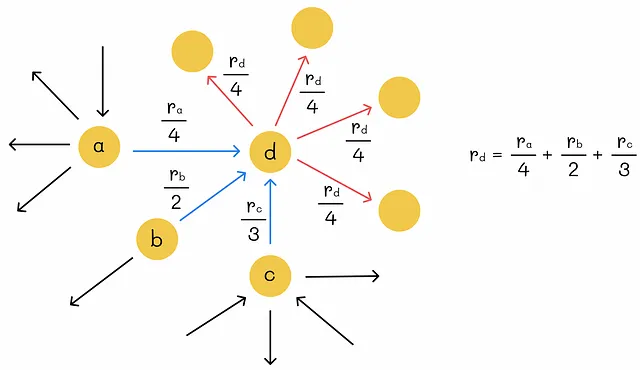
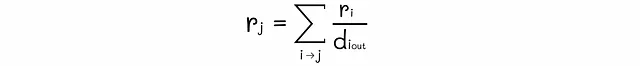
n個のウェブページのグラフが与えられた場合、グラフの重みを求めるためにn個の連立方程式を作成することができます。しかし、そのようなシステムには無限の解が存在する可能性があります。そのため、一意の解を課す別の制約を追加する必要があります。ちなみに、PageRankは、すべてのノードの重要性の合計が1に等しいという正規化条件を追加します。

解決策を見つけましたが、スケーラブルではありません。ガウスの消去法を使っても、O(n³)の計算量になります。分析されるウェブページの数nが数十億に達する可能性があることを考慮すると、より効率的なアプローチを考える必要があります。

まず、表記を簡素化しましょう。そのために、リンクされたウェブページの各ペアのリンクの重みを含む隣接行列Gを導入します（2つのウェブページがリンクされていない場合、対応する行列要素には0を入れます）。より正式には：

行列Gは確率的と呼ばれます。なぜなら、それぞれの列の合計が1になるからです。

次に、ランクベクトルrを定義します。このベクトルのi番目の要素は、ページiのランク（重要度）と等しいです。このベクトルのすべての要素の合計も1になります。私たちの究極の目標は、このベクトルrの値を見つけることです。

PageRank方程式

行列Gをベクトルrと乗算すると、同じベクトルrが得られることが分かります。前のセクションのグラフの例に基づいて、そのような結果が得られることがわかります。

なぜそうなるのでしょうか？偶然ではありませんか？行列Gのi番目の行には、ページiへのすべての入力リンクの重みが含まれています。i番目の行のj番目の要素をr[j]と乗算すると、実際には成分rj / d[j]out（ノードjからiへの重要性）が得られます。ノードiとjの間にリンクがない場合、対応する成分は0に設定されます。論理的には、ベクトルrとi番目の行の乗算の最終結果は、グラフの任意の接続されたノードからノードiへのすべての重要性の合計に等しいはずです。定義によれば、この値はノードiのランクに等しいです。一般的には、次の方程式を書くことができます：

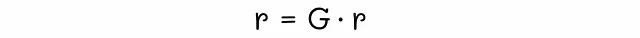
したがって、目標は、入力行列Gと乗算しても同じままであるようなベクトルrを見つけることです。

固有ベクトル

線形代数学の固有ベクトルに関する理論を見直すことで、上記の方程式の解を見つけることができます。行列Aが与えられた場合、ベクトルvは固有ベクトルと呼ばれます。以下の方程式を満たす数αが存在する場合、その数αは固有値と呼ばれます。

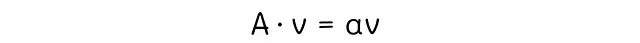
数αは固有値と呼ばれます。PageRank方程式は、行列A = G、ベクトルv = r、α = 1に対応していることに気付くことができます。通常、正方行列にはいくつかの固有値と固有ベクトルがありますが、行列Gは確率的であるため、その最大固有値は1となるという理論が主張しています。

べき乗法

行列の固有ベクトルを見つける最も人気のある方法の1つは、べき乗法です。これは、初期ベクトルrをいくつかの値で初期化することから始まります（ここではウェブページの数nで1 / nを使用します）。その後、常にG * rの値を計算し、この値を再びrに割り当てます。ベクトルrとG * rの距離がある閾値ε未満になる任意の反復で、アルゴリズムを収束成功として停止します。

上記の例では、εを0.0005に設定すると、アルゴリズムは正しく9回の反復で収束します：

明らかに、これはただのおもちゃの例ですが、実際には、この方法はより多くの変数に対しても非常にうまく機能します。

ランダムウォーク

時刻tでグラフの任意のノードにいるとすると、ウォーカー（サーファー）を想像してください。p(t)をベクトルとし、i番目の成分が時刻tでノードiにいる確率であるとします。その後、サーファーはランダムに（等しい確率で）現在のノードにリンクされた別のノードを選択し、時刻t + 1にそこに移動します。最終的に、時刻t + 1の分布ベクトルp(t + 1)を見つけたいとします。

サーファーが時刻t + 1にノードiに現れる確率は、以前に隣接ノードjにいた確率（iへの移動の確率を乗じた）の確率（jへの移動の確率）の合計となります。

• サーファーが時刻tでノードjに現れる確率はp(t)[j]です。
• ノードjからiへの移動の確率はG[j][i]と等しいです。

これらの確率を合計することで、p(t + 1)[i]の値を得ることができます。すべてのグラフノードのp(t + 1)の値を見つけるために、同じ方程式を行列形式で書くことができます：

この方程式は、以前にPageRankで得たものとまったく同じ形をしています！これは、これらの2つの問題が同じ解と解釈を持つことを意味します。

ある時点で、分布ベクトルp(t)は収束します：p(t + 1) = M * p(t) = p(t)。この場合、収束したベクトルp(t)は定常分布と呼ばれます。時間の経過に伴い、任意のノードに滞在する確率は変化しません。

ノードのPageRankスコアは、グラフをランダムに移動することによって将来、サーファーがこのノードに存在する確率と等しいです。

収束

グラフ全体を通じての移動のプロセスは、しばしば「マルコフ連鎖」と呼ばれます。マルコフ連鎖理論には、以下のような定理が存在します：

グラフ構造に特定の条件がある場合、定常分布は一意であり、時刻t = 0で任意の初期確率分布で到達できます。

次のセクションでは、一意の収束を達成するために満たす必要がある条件について詳しく説明します。すべてのグラフで一意の収束が達成できるわけではないことがわかります。

基本的に、避ける必要がある2つのケースが存在します。

行き止まり

出力リンクを持たないノードは行き止まりと呼ばれます。このようなノードの問題は、ネットワークからの総合的な重要性が漏れ出してしまうことです。以下に例を示します：

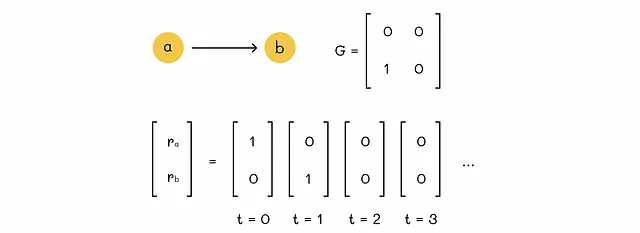
スパイダートラップ

ノードのグループが他のノードに出リンクを持たない場合、それらはスパイダートラップを形成します。基本的に、一度入ると、このノードグループから抜け出すことは不可能です。スパイダートラップは次の2つの問題を引き起こします：

• アルゴリズムは決して収束しません。
• スパイダートラップを形成するノードグループは、グラフの重要性をすべて取り込みます。その結果、これらのノードは非常に重要であり、他のノードは重要性が0となります。

最初の問題は以下の図で示されています：

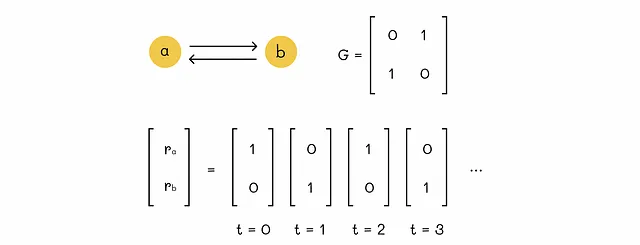
重要性の取り込みは次の図で示されています。以下のおもちゃの例では、重大な問題ではないように見えるかもしれませんが、スパイダートラップを形成するウェブページが数百万あるウェブネットワークを想像してみてください。その結果、これらの数ページは利用可能な重要性をすべて配分し、他のすべてのウェブページの重要性は0に設定されます。明らかに、これは現実的には望ましくありません。

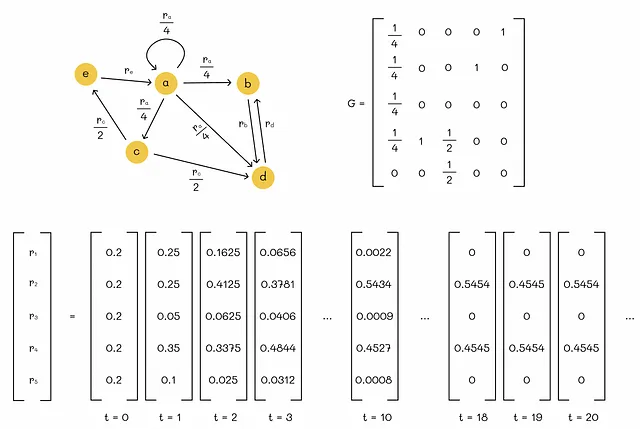
テレポート

Googleが提案する解決策の1つは、サーファーの各移動の前に次の条件を追加することです：

• 確率βで、他のリンクされたノードに移動します。
• 確率(1 — β)で、ランダムなノードに移動します（テレポートを介して）。

パラメータβはダンピングファクターと呼ばれます。元のPageRankアルゴリズムの著者は、βの値を0.85とすることを推奨しており、平均して5つの遷移後にサーファーがランダムに他のノードにジャンプすることを意味します。アイデアは、サーファーがスパイダートラップに落ちた場合、ある時点でテレポートを通じてそこから抜け出すことができるというものです。

以下の図は、テレポートがスパイダートラップの問題に対処するのにどのように役立つかを示しています。サーファーがノードcに入ると、そこに永遠にとどまるでしょう。テレポート（青い線）を導入することで、この問題を解消し、サーファーがある時点で別のランダムなノードに移動することを保証します。

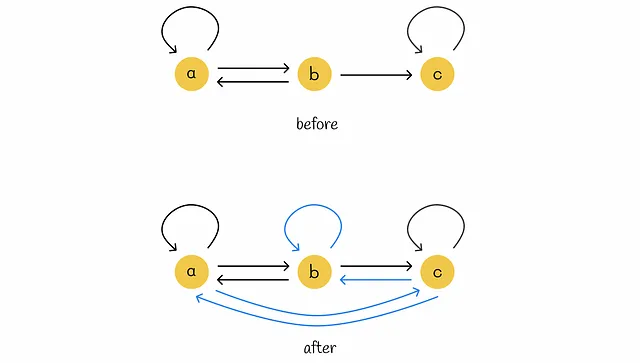
ただし、行き詰まりのノードにはアプローチをわずかに変更する必要があります。上記の例の1つからわかるように、行き詰まりはグラフ内での重要性漏れを引き起こします。この現象は、初期行列Gの対応するゼロ列によって、ランクベクトルがゼロで埋め尽くされることでパワー反復法の間に観察されることができます。最終的に、以下のようなことができます：

サーファーが行き止まりのノードにたどり着いた場合、グラフのランダムなノード（等しい確率で）にすぐに移動する必要があります。

実際には、この条件を満たすために初期行列 G を変更することができます。行列 G のすべての行の行末ノードに対応する列の要素のゼロを 1/n に置き換えるだけです。以下の例は、この原則を示しています。

ノード c は行列 G のゼロの列を持つ行き止まりのノードです。c からグラフのすべてのノードへの n = 3 のテレポートを追加することで、c から任意のノードに移動する確率 p = 1/3 が等しくなります。これを考慮に入れるために、ノード c に対応する行列 G の列を値 1/3 で埋めます。

テレポートを追加することにより、行列のすべての列の合計が 1 になることがわかります。言い換えると、行列 G は確率的になります。これは後で使用する重要な特性です。

収束条件

マルコフ連鎖の理論から重要な定理が存在します。この定理は収束条件を定義しています。

任意の始状態ベクトルに対して、遷移行列 G は一意の正の定常分布ベクトル r に収束する場合、G に対応する連鎖が確率的で非周期的かつ既約であるとします。

この定理で最後の 3 つの特性を思い出し、導入されたテレポートが上記の問題を解決するかどうかを確認しましょう。

連鎖 G が「確率的」と呼ばれる場合、各列の合計が 1 に等しいことです。

前述の通り、テレポートを行き止まりのノードに追加することで、行列のゼロの列がなくなり、すべての列の合計が 1 になります。この条件は既に満たされています。

連鎖 G が「周期的」と呼ばれる場合、任意のノード間のパスの長さは常に k の倍数となる数 k > 1 が存在します。それ以外の場合、連鎖は非周期的と呼ばれます。

この条件は、同じ状態への戻りが k の倍数で発生する必要があることを意味します。非周期性の場合、戻りは不規則なタイミングで発生します。基本的に、この条件はスパイダートラップの問題を指します。テレポートを追加することでスパイダートラップの問題を解決しているため、連鎖 G は非周期的です。

連鎖 G が「既約」と呼ばれる場合、あるノードから別のノードへの遷移確率は常に 0 より大きくなります。

この条件は、任意の 2 つのノード間にリンクが存在することを意味します。つまり、どのノードにも固執することはできません。言い換えると、行列 G はすべてのゼロでない要素で構成されている必要があります。以下の次のセクションで、これがグラフのすべてのノードを接続することで満たされる方法を見ていきます。

アルゴリズムの変更

Google が提案する PageRank アルゴリズムは、初期行列 G を取り、行き止まりから他のノードへのテレポートを追加して調整します。これにより確率的性質が保証されます。非周期性と既約性を保証するために、各ノードに以下の条件を追加します：

• 確率 β で別のリンクされたノードに移動する。
• 確率 (1 — β) でランダムなノードに移動する。

数学的には、次のようなランク方程式が各ノードに対して得られます：

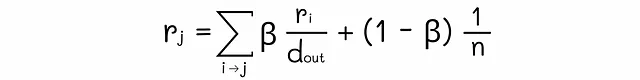
この方程式を行列形式に変換することができます：

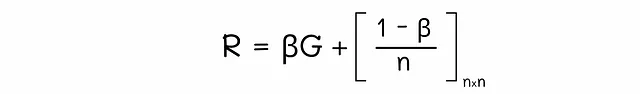
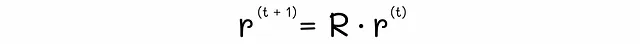
上記の例の1つから、修正されたグラフと対応する遷移行列Rを描画してみましょう：

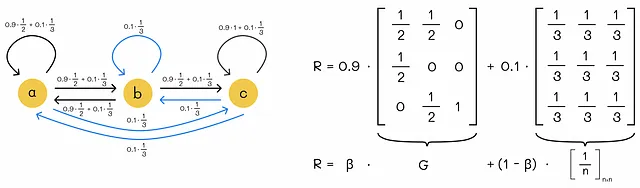
効率の向上

私たちに残されている唯一の問題は、遷移行列Rをどのように保存するかです。Rはサイズがn x nの正方行列であり、nはウェブページの数です。現在、Googleは25億以上のウェブページを持っています！行列Rには0が含まれていないため、密であり、完全に保存する必要があります。1つの行列要素を保存するために4バイトが必要とすると仮定しましょう。行列Rを保存するために必要な総メモリサイズは(25 * 10⁹)² * 4（バイト）〜3 * 10²¹（バイト）です。これは膨大なメモリサイズです！少なくともいくつかの桁を削減する別のアプローチを考える必要があります。

まず、テレポートを追加することは、初期の行列Gの要素を(1 – β)% 減らし、それらを均等にすべてのノードに分散させることと等価であることに気づくことができます。これを心に留めて、PageRankの行列方程式を別の形式に変換することができます：

最後に得られた方程式を見てみましょう。Gは、ほとんどの要素が0である初期のリンク行列です。なぜそうなのでしょうか？実際には、任意のウェブページを取ると、おそらく他の数十のウェブページへのリンクしか含まれていないでしょう。25億以上のウェブページがあることを考慮すると、ウェブページの数に対する総リンク数の相対的な数は非常に小さいです。したがって、Gには多くのゼロが含まれており、Gは疎です。

疎行列の保存には、密行列よりもはるかに少ないメモリが必要です。各ウェブページが平均して他の40ページにリンクしていると仮定しましょう。行列Gを保存するために必要な総バイト数は、25 * 10⁹ * 40（バイト）= 10¹²（バイト）= 1（TB）となります。Gを保存するためにはわずか1テラバイトしか必要ありません。以前と比べて、これは素晴らしい改善です！

実際には、各反復では、行列Gとベクトルrの乗算を計算し、それをβで乗算し、結果のベクトルの各要素に(1 – β) / nの定数を追加するだけです。

また、初期のチェーンGに行き詰まりのノードが含まれている場合、各反復でベクトルrの合計値は1よりも小さくなります。これを解決するために、それを再正規化するだけで十分です。つまり、すべてのベクトルの要素の合計が1になるようにします。

完全なアルゴリズム

以下の図では、PageRankアルゴリズムの完全なバージョンが表示されています。各反復では、ランクの更新は2つのステージで行われます。最初のステージでは、初期行列Gに従ってのみ更新が行われます。次に、ランクベクトルの要素を変数sに合計します。これにより、(1 – s)の値は、単一ノードの総入力ランクが減少した値です。これを補うために、2番目のステージでは、テレポートを考慮し、(1 – s) / nの値を持つノードからすべてのノードに追加します。

結論

この記事では、PageRankアルゴリズムのさまざまな定式化を調べ、最終的に最適化されたバージョンを見つけました。他の検索結果のランキング方法の存在と進化にもかかわらず、PageRankはGoogleの検索エンジンの裏で動作する他のアルゴリズムの中で最も効率的なアルゴリズムのままです。

参考文献

この記事の論理的な構造は、スタンフォード大学の大規模グラフに関する講義に基づいています。

• 大規模グラフの解析：リンク解析、PageRank
• 大規模データセットのマイニング | Jure Leskovec、Anand Rajaraman、Jeff Ullman
• PageRank：巨人の肩に立つ

特記されていない限り、すべての画像は著者によるものです

We will continue to update VoAGI; if you have any questions or suggestions, please contact us!